Area Of Hexagon Given Radius

In geometry, a hexagon is a 2-dimensional closed shape with 6 sides. There are two kinds of hexagons based on the lengths of the sides and the angles they form, namely regular hexagons, irregular hexagons, convex hexagons, and concave hexagons. A regular hexagon is a hexagon with equal side lengths and each of its interior angles is 120°. An irregular hexagon is a hexagon whose measurements of side lengths and angles are dissimilar. A concave hexagon is a hexagon with at to the lowest degree one interior angle that is greater than 180°. A convex hexagon is a hexagon with no angle pointing inwards; i.due east., the measure of every interior bending is less than 180°.

Area of a hexagon

The surface area of the hexagon is referred to as the surface area enclosed by its six sides.

The formula for the area of a regular hexagon is

The area of a regular hexagon = $\frac{3\sqrt{3}}{2}a^{2}$

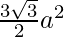
In a regular hexagon, the radius (r) of a hexagon is equal to the length of its side (a), i.e., a = r. Thus, the regular hexagon is divided into six equilateral triangles.

At present,

The expanse of a regular hexagon with radius "r" = $\frac{3\sqrt{3}}{2}r^{2}$

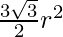
Derivation

To derive the area of a regular hexagon, dissever it into half dozen triangles past joining its reverse vertices with a line segment.

Each triangle is an equilateral triangle with its side length "a" and height √3a/2 (which is besides the apothem of the hexagon).

Nosotros know that,

The expanse of a triangle = ½ × base × summit

=½ × a × (√3a/2)

The area of a triangle = √3a²/iv

Since there are vi equilateral triangles

The area of a regular hexagon = six × (Surface area of the equilateral triangle)

A = half-dozen × (√3a²/4)

A = $\frac{3\sqrt{3}}{2}a^{2}$

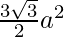
In a regular hexagon, the length of the side (a) is equal to the radius of the hexagon (r)

Hence,

The area of the regular hexagon = $\frac{3\sqrt{3}}{2}r^{2}$

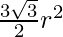
Sample Bug

Problem i: Find the area of a regular hexagon with a radius of half dozen in.

Solution:

Given,

The radius of the regular hexagon (r) = vi in

We know that the radius of a regular hexagon is equal to the length of each side of the hexagon.

(Length of the side of a regular hexagon) a = r

The expanse of the hexagon = 3√3r²/2

⇒ A = three√three(half dozen)²/2

⇒ A = 3√3(36)/ii

⇒ A = 54√3 sq. in

Hence, the surface area of the hexagon is 54√iii sq. in.

Problem 2: Make up one's mind the radius of the hexagon if its area is 96√iii sq. cm.

Solution:

Given,

The area of the hexagon = 96√iii sq. cm

We know,

The area of the hexagon = 3√3a²/2

⇒ 96√3 = three√3a²/2

⇒ a^two = 96√3 × (2/3√3)

⇒ a² = 64 ⇒ a = √64

⇒ a = 8 cm.

Nosotros know that the radius of a regular hexagon is equal to the length of each side of the hexagon, i.e., a = r = 8 cm

So, the radius of the regular hexagon (r) is 8 cm.

Problem 3: Find the area of the hexagon whose radius is 12 units.

Solution:

The radius of the regular hexagon (r) = 12 units

We know that the radius of a regular hexagon is equal to the length of each side of the hexagon.

(Length of the side of a regular hexagon) a = r

The surface area of the hexagon = three√3a²/ii

⇒ A = iii√3(12)²/2

⇒ A = 3√3(144)/2

⇒ A = 216√3

⇒ A = 374.112‬‬ square units

Hence, the area of the hexagon is 374.112‬ square units.

Trouble 4: Calculate the radius of the hexagon if its area is 24√3 sq. in.

Solution:

Given,

The surface area of the hexagon = 24√3 sq. cm

We know,

The area of the hexagon = three√3a²/2

⇒ 24√3 = 3√3aⁱⁱ/2

⇒ a^two = 24√3 × (two/3√3)

⇒ aⁱⁱ = xvi ⇒ a = √sixteen

⇒ a = 4 cm.

We know that the radius of a regular hexagon is equal to the length of each side of the hexagon, i.e., a = r = 4 cm

So, the radius of the regular hexagon (r) is iv cm.

Problem 5: Calculate the expanse of the hexagon if its perimeter is 54 cm.

Solution:

Given,

The perimeter of the hexagon = 54 cm.

We know that the perimeter of a hexagon = 6a

⇒ 6a = 54 ⇒ a = 54/half dozen

⇒ a = nine cm

We know that the radius of a regular hexagon is equal to the length of each side of the hexagon

Hence a = r = vi cm.

The expanse of the hexagon = iii√3a²/ii

A = 3√3(9)ⁱⁱ/2

A = iii√3(81)/2 = 121.5‬√3

A = 121.5 × 1.732 = 210.438‬ sq. cm

Hence, the area of the hexagon is 210.438‬ sq. cm.

Problem 6: Calculate the expanse of a regular hexagon whose radius is three units.

Solution:

The radius of the regular hexagon (r) = 3 units

The area of the hexagon = 3√3r²/2

⇒ A = three√3(3)²/two

⇒ A = 3√three(9)/ii

⇒ A = (thirteen.5)√iii square units

⇒ A = 23.382‬ foursquare units

Hence, the area of the hexagon is 23.382‬ foursquare units.